Pure and simple transaction memories

Now for a technical article.

How can several parallel programs maintain a consistent view of state. By this I mean how can two programs, possibly in different countries, manipulate common state variables in a consistent manner? How can they do so in a way that does not involve any locking?

The answer is surprisingly simple and incredibly beautiful and makes use of something called a transaction memory.

How do transaction memories work?

To start with I must explain why concurrent updates to data represents a problem.

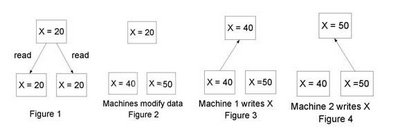
Imagine a server S with some state variable X and two clients C1 and C2. The clients fetch the data from the server (figure 1). Now both clients think that X=20. C1 increases X by 20 and C2 increases X by 30. They modify their local copies, (figures 2) and write the data back to the server (figures 2 and 3). If these updates had been performed one after the other then the final value of X stored on the server would have been 70 and not 50 obviously something has gone wrong.

The conventional way to solve this problem is to lock the server while the individual transactions are taking place, but this approach is thwart with problems as I have pointed out in an earlier article.

To allow these updates to proceed in parallel and without recourse to locking, we can make use of a so called transaction memory.


Transaction Memory

A transaction memory is a set of tuples (Var,Version,Value). In the diagram X has version 1 and value 20. Y has version 6 and value true.

The version number represents the number of times the variable has changed.

Now let's try and do a transaction. Suppose we want to change X and Y. First we send a {get,X,Y} message to the server. It responds with the values of the variables and their version numbers.

Having changed the variables we send a {put,(X,1,30),(Y,6,true)} message back to the server. The server will accept this message only if the version numbers of all the variables agree. If this is the case then the server accepts the changes and replies yes. If any of the version numbers disagree, then it replies no.

Clearly if a second process manages to update the memory before the first process has replied then the version numbers will not agree and the update will fail.

Note that this algorithm does not lock the data and works well in a distributed environment where the clients and servers are on physically different machines which unknown propagation delays.

Isn't this just the good old test-and-set operation generalised over sets?

Yes - of course it is. If you think back to how mutexes were implemented they made use of semaphores. Semaphores were implemented by an atomic test-and-set instruction. A semaphore can only have the value zero or one. The test-and-set operation said if the value of this variable is zero then change it to one this operation was performed atomically. To reserve a critical region it was protected by a flag. If the flag was zero then it could be reserved, if the flag was one then it was being used. To avoid two processes simultaneously reserving the region test-and-set must be atomic. Transaction memories merely generalise this method.

Now let's implement this in Erlang:

-module(tm).

-export([new/0, addVar/2, getVars/2, putVars/2]).

%% new() -> Pid
%%   create a new transaction memory (TM)
%%
%% addVar(Pid, Var) -> ok
%%   add a variable to the TM store
%%
%% getVars([V1,...]) -> [{Vsn,Data},....]
%%   lookup variables v1,V2, ... in the TM
%%
%% putVars([{Var,Vsn,Data}]) -> Bool
%%   update variables in TM


%% Heres a sample run
%%
%% 1> c(tm).
%% {ok,tm}
%% 2> P=tm:new().
%% <0.47.0>
%% 3> tm:addVar(x).
%% ok
%% 4> tm:addVar(P,x).
%% ok
%% 5> tm:addVar(P,y).
%% ok
%% 6> tm:getVars(P, [x,y]).
%% [{ok,{0,void}},{ok,{0,void}}]
%% 7> tm:putVars(P, [{x,0,12},{y,0,true}]).
%% yes
%% 8> tm:putVars(P, [{x,1,25}]).       
%% yes
%% 9> tm:getVars(P, [x,y]).            
%% [{ok,{2,25}},{ok,{1,true}}]
%% 10> tm:putVars(P, [{x,1,15}]).
%% no

new() -> spawn(fun() -> loop(dict:new()) end).

addVar(Pid, Var) -> rpc(Pid, {create, Var}).

getVars(Pid, Vgs) -> rpc(Pid, {get, Vgs}).

putVars(Pid, New) -> rpc(Pid, {put, New}).

%% internal
%%
%% remote procedure call

rpc(Pid, Q) ->
   Pid ! {self(), Q},
   receive
       {Pid, Reply} -> Reply
   end.

loop(Dict) ->
   receive
     {From, {get, Vars}} ->
        Vgs = lists:map(fun(I) ->
                 dict:find(I, Dict) end, Vars),
        From ! {self(), Vgs},
        loop(Dict);
     {From, {put, Vgs}} ->
        case update(Vgs, Dict) of
        no ->
                From ! {self(), no},
                  loop(Dict);
        {yes, Dict1} ->
                From ! {self(), yes},
                loop(Dict1)
        end;
    {From, {create, Var}} ->
       From ! {self(), ok},
       loop(create_var(Var, Dict))
   end.

update([{Var,Generation,Val}|T], D) ->
    {G, _} = dict:fetch(Var, D),
    case Generation of
     G -> update(T, dict:store(Var, {G+1, Val}, D));
     _  -> no
    end;
update([], D) ->
    {yes, D}.

create_var(Var, Dict) ->
    case dict:find(Var, Dict) of
   {ok, _} -> Dict;
   error -> dict:store(Var, {0,void}, Dict)
    end.

Why I don't like shared memory

In my last blog concurrency is easy I wrote about a simple model for programming concurrent systems. When you write a blog you have to think about the target audience and what level you want to pitch the blog at. Should it be technically advanced, or should it popularise the ideas you want to talk about?

I chose to talk about concurrency in a decidedly non-technical manner, I thought I'd use the analogy of people talking to each other. In my blog I argued that processes should behave pretty much like people. People have private memories and exchange data by message passing.

Now reactions to this were beyond my expectations. To start with a lot of people read what I'd written - this came as a surprise. Hardly without publicising the article it reached the #3 stop on programming.reddit.com - indeed last Wednesday three of the top five programming articles on reddit.com were about Erlang. Secondly a discussion thread started on reddit.com where people discussed what I'd written.

Here I'm going to answer the first point that was raised in the discussion thread:

---

"dogger" said this:

I'm not sure I quite got why not having shared memory was so great. His example of throwing simple question/answer messages around isn't really how lots of programs work. I think sending messages has its place, as does shared memory. Choose which ever one is most appropriate.

---

Good comment! the things that we take for granted are the things we feel the least need to explain. Now I take the view that sharing memory is wrong. Having thought this way for the last twenty odd years I take this as axiomatic, and never really explain why I think shared memory is a bad idea - so in what follows I'll give are a number of reasons why I don't like sharing memory.

Dogger's second comment "His example ... isn't really how lots of programs work" Is of course, correct. Lots of programs do not work in the way I have suggest, the point is that these program could have been written in a different programming style which totally avoids shared memory and locks and which does make use of fine-grain concurrency and pure message passing. I also believe that such programs are much easier to write and understand since all of the problems with shared memory that I list below are sidestepped. Note that I do not suggest that I have a solution to any of the problems below. But I would say that such problems can be avoided altogether by using a different programming style.

Now I'll turn to why I don't like shared memory:

Problem 1 - Programs that crash in a critical region

The following approach is commonly used when two or more programs wish to share memory. Any program that wishes to manipulate shared memory, must do the following:

1. Acquire a lock
2. Manipulate the shared memory
   
3. Free the lock

The code that the program executes after acquiring the lock and before freeing it is called the critical region.

During the time that the program is inside a critical region it should not crash, and it should not spend too much time inside the critical region.

But what happens if the program does crash inside the critical region?


In this case things get messy. In an ideal world we would like to have some kind of transaction semantics, meaning that the net effect of running the program would be either that all the memory changes made inside the critical region succeeded or none of them succeed and the state of memory is the same as it was before the program entered the critical region.

Suppose that A tries to change 10 memory locations, I'll call them M1,M2,...,M10, and that the program was supposed to do this:

1. Acquire a lock
2. Modify M1
3. Modify M2
4. ...
5. Modify M10
6. Release the lock

But in fact it did this:

1. Acquire a lock
2. Modify M1
3. Modify M2
4. Crash
   

We would like the effect of running A to be that either is succeeded and all the memory changes M1 to M10 took place, or that none of them succeeded. So having crashed at step 4 of the above we would like to undo the effect of the first two modifications of memory.

Achieving this is pretty complicated, it assumes that there is some monitor program that can detect that a thread has crashed and which reset the memory to its original state in the event of a crash.

Problem 2 - Programs that spend too long time in the critical region

A number of things can happen when a program is inside a critical region, it can manipulate memory, which is why it must be in the critical region in the first place, and it can perform computations. The problem is that these computations take place while the program is inside the critical region - so if these computations take a long time, then all other programs waiting to access the shared memory will be queued until the current program has left the critical region.

Writing code that executes inside the critical region can be very difficult, since we have avoid very time consuming computations and move them outside the critical region. We also have to remove things like remote procedure calls from the critical region, in case they should suddenly take too long. All of this is a very unnatural way of programming and extremely difficult to get right.

Problem 3 - Locking too much

Unfortunately we often lock far more memory than we need to, a program will typical lock all the shared memory, just to manipulate one tiny fragment of it. In languages which permit direct memory modification through pointers then the minimum size of memory that can be protected is determined by the granularity of the page tables. A typical page size might be in the range 8-64KB - with a page size of 8K you might only want to protect a single byte, but you are forced to protect a minimum of 8KBytes.

Your program might only need to protect 1 Byte, and the other programs in the system might wish to modify some other parts of memory in the same page, yet these have to wait until your program as left its critical region before they can manipulate their portion of the memory.

Now all of this probably doesn't matter on a single CPU where different threads all run on the same CPU, the CPU is always busy and at least its doing something. But on a multi-core CPU it does matter. On a multi-core CPU many of the processes will be waiting to acquire locks despite the fact that logically all these CPUs could be running in parallel.

We could, of course, divide the shared memory into different partitions, and let the program lock onto those parts of memory they were interested in, but now the programming gets even more difficult.

Problem 4 - Distributed shared memory

Now things get really messy. On a single motherboard there really can be a single memory that a number of different CPUs can access, but on a cluster or in a networked distributed system this is just infeasible. What really happens is that each node in the system has its own memory and that reads and writes and locks are applied to the local memory. In any system one of these memories must assume some kind of master role, the other memories in the system assume secondary roles and behave as caches. Then some kind of cache consistency protocol is run between the different memories to ensure that all the processes accessing this memory have a consistent view of the world.

Now all of this is very difficult to achieve - so at this point most programmers just give up and use a fault tolerant distributed database, which is generally pretty slow since it has to do a lot of messy things in the background.

Problem 5 - Sharing limits scalability

Threads which share data cannot run independently and in parallel. Now this doesn't matter on a single-core CPU, but it does matter no a multi-core CPU. At the point in their execution where the threads share data, their execution becomes serial rather than parallel. The critical regions in the threads introduce serial bottlenecks which limits scalability.

If we want really high performance we have to make sure that our applications share nothing, that way we can just replicate our solution over many independent CPUs.

Problem 6 - Sharing can introduce deadlocks

Sometime we try to increase concurrency by some form of fine-grain sharing. The idea is that instead of locking all our memory, we divide the memory into smaller regions and only lock those parts of memory we are interested in. Imagine now two threads P and Q which want access to memory regions A and B. Suppose P locks memory region A and then waits for memory region B, and Q does the opposite, ie it locks first B then waits for A. This results in a deadlock, P and Q now suspend indefinitely

Problem 7 - Sharing makes systems error prone and debugging difficult

Suppose two threads A and B share data. A mistake in A can overwrite data used by B. Even through the code in B was correct it might crash because the data structures it manipulates have been corrupted by A. Now all systems should ideally obey the my program should not be able to crash your program rule - this is clearly not the case when programs can share data.

Debugging becomes horrific. Thread B has crashed, so it seems reasonable to assume that the code for thread B is incorrect - this assumption is wrong, since the code in A is to blame. This separation of cause and effect makes debugging very difficult.

Finally a more general comment

Sharing doesn't exist in the real world

I'm an ex physicist. In classical physics and ignoring quantum effects two objects in the real world cannot exist in the same place at the same time.

If we have two objects they must be at different places. Now the only way one object can interact with another is by sending it a message (say by a light ray). If this light ray encodes some information about a state change, then as far as the receiving object is concerned the state change only becomes known after the message has been received.

In simple relativity theory the concept of simultaneity just does not exist.

The point is that in reality objects do not share state, I believe its not a good idea to model what cannot exist in reality in software.

The idea that you actually need sharing and locks to implement parallel software is false. Everything that can be achieved with sharing and locks can also be achieved with pure message passing and no locks. The is the Erlang way.

---

In a future posting I'll tell you how to make a transaction memory which provides a lock-free method of achieve fine-grain state consistency in sets of parallel processes.

Concurrency is easy

We understand concurrency

A deep understanding of concurrency is hard-wired into our brains. We react to stimulation extremely quickly, in a part of the brain called the amygdala, without this reaction system we would die. Conscious thought is just too slow, by the time the thought "hit the brakes" has formed itself, we have already done it.

On a motorway, I mentally track the positions of dozens, or hundreds of cars, this is done without conscious thought. If I couldn't do this I would probably be dead.

The world is parallel

If we wish to write programs that behave as other objects behave in the real world then these programs will have a concurrent structure.

This is why we should program in a concurrent programming language

And yet most often we program real-world applications in sequential programming languages. This is uncessarily difficult.

By programming in a language what was designed for programming concurrent applications (like Erlang) concurrent programming becomes a lot easier.

Erlang programs model how we think and interact

We don't have shared memory. I have my memory, you have yours, we have two brains, one each, they are not joined together. To change your memory I send you a message, I talk or wave my arms. You listen, you see, your memory changes, but without asking you a question or observing your response I do not know that you have received my messages.

This is how it is with Erlang processes. Erlang processes have no shared memory. Each processes has its own memory. To change the memory of some other process you must send it a message and hope that it receives and understands the message.

To confirm that another process has received your message and changed its memory, you must ask it (by sending it a message). This is exactly how we interact.

Sue: "Hi Bill, my telephone number is 45 67 89 12"

Sue: "Did you hear me?"

Bill: "sure, your number is 45 67 89 12"

These interaction patterns well-know to us, from birth onwards we learn to interact with the world by observing it and by sending it messages and observing the responses.

People function as independent entities that communicate by sending messages

That's how Erlang processes work, and that's how we work so it's very easy to understand an Erlang program.

Erlang programs are made up of lots of little processes all chattering away to each other - just like people.

An Erlang program is made up of dozens, possible thousands or even hundreds of thousands of small processes - all these processes operate independently. They communicate with each other by sending messages. Each process has a private memory. They behave like a huge room of people all chattering away to each other.

This makes Erlang program inherently easy to manage and scale. Suppose we have ten people (processes) and they have too much work to do, what can we do? get more people. How can we manage these groups of people, easy just shout instructions at them (broadcasting).

Erlang processes don't have shared memory, so there is no need to lock the memory while it is being used. Where there are locks, there are keys, and when there are keys the keys will one day get lost and what happens when you loose a key? - you panic.

Distributed software systems with locks and keys always go wrong.

If somebody dies other people will notice

I I'm in a room and suddenly keel over and die, somebody will probably notice, well at least I hope so. Erlang processes are just like people, they can on occasions die. Unlike people when they die they shout out in their last breath exactly what they have died from.

Imagine a room full of people, suddenly one person will keel over and die and just as they die, they say "I'm dying of a heart attack" or "I'm dying of an exploded gastric wobbledgog". That's what Erlang processes do. One process might die saying.

"I'm dying because I was asked to divide by zero", another might say

"I'm dying because because I was asked what the last element in an empty list was"

Now in our room full of people we might imagine there are specially assigned people whose job it is to clear away the bodies. Let's imagine two people Jane and John. If Jane dies then John will fix any problems associated with Jane's death. If Jane dies then John will fix the problems. Jane and John are linked together with an invisible agreement which says that if one of them dies the other will fix up any problems caused by the death.

That's is how error detection in Erlang works, processes can be linked together. If one of the processes dies, the other process gets an error message saying why the first process dies.

That's basically it.

That's how Erlang programs work.

What we've learnt so far

Erlang programs are made of lots of processes. These processes can send messages to each other.

These message may or may not be received and understood. If you want to know if a message was received and understood you must send the process a message and wait for a reply.

Pairs of processes can be linked together. If one processes in a linked pair dies the other process in the pair will be sent a message containing the reason why the first process died.

This simple model of programming is part of a model I call Concurrency Oriented Programming. You can read more about this here.